Randomized experiments (e.g. A/B testing, RCTs) are great. A simple treatment versus control experiment in which all units have the same probability of treatment assignment ensures that receiving a treatment is not systematically correlated with any observed or unobserved characteristics of the experimental units. For example, there may be differences in mean covariates between treatment and control groups, but this is already accounted for in standard statistical inference about treatment effects.

However, randomization can cause problems. Often this can be understood as some version of potential non-compliance or attrition. Some units are allocated for processing, but downstream items ignore them and the original allocation is lost (a kind of potential non-compliance). Alternatively, if an inconsistency is detected, downstream may delete that observation from the data. Alternatively, processing may result in a unit (e.g., app user) being terminated immediately (e.g., app crashing) and the unit not recorded as having been exposed to the experiment.

Therefore, it would be a good idea to check whether some key summaries of the task are extremely implausible under the assumed randomization. For example, you can perform a joint test for differences in covariates before treatment. or – This is especially useful when there are no or many covariates. You can test whether the number of units in each treatment matches the planned (e.g. Bernoulli (1/2)) randomization. In the tech world, this is also known as ‘sample rate mismatch’ (SRM) testing.

This kind of problem is very common. One very common way this happens is from the streaming arrival of the randomization unit to the point where the treatment is applied. This is unavoidable if the user is not logged in. If you have a world of user accounts, randomly processing all of them and using them as analysis samples may still be a dead end. Most of these users will have never touched the part of the Service to which processing applies. . Therefore, it is common to instead trigger logging for experimental impressions and analyze only a sample of those users (which may be less than 1% of all users). It’s very common to use this kind of “triggering” or exposure logging, but it can also cause problems. For example, we analyzed experiments on several Microsoft products and found that: Approximately 6% of such trials had sample rate discrepancies. (at p<0.0005).

Another example of randomization problems associated with public data is:

Upworthy Research Archives

Nathan Matias, Kevin Munger, Marianne Aubin Le Quere and Charles Ebersole collaborated with Upworthy to curate and launch. Dataset consisting of over 15,000 experiments and a total of over 150,000 treatments. Each of these experiments modifies the headline or image associated with an article on Upworthy, as seen when viewing other focused articles. The result is that people click on these headlines. You may remember Upworthy as a major innovator of “clickbait,” especially clickbait with a particular ideological bent.

One of the things I really like about the way they released this data is that they initially only created a subset of the experiments that could be used as an exploratory data set. This allowed researchers to perform an initial analysis on that data and then preregister analyzes and/or predictions on the remaining data. To me, this usefully highlighted that sometimes the best way to make a data set available as a public good is to structure how it is made available, rather than providing it all at once.

randomization problem

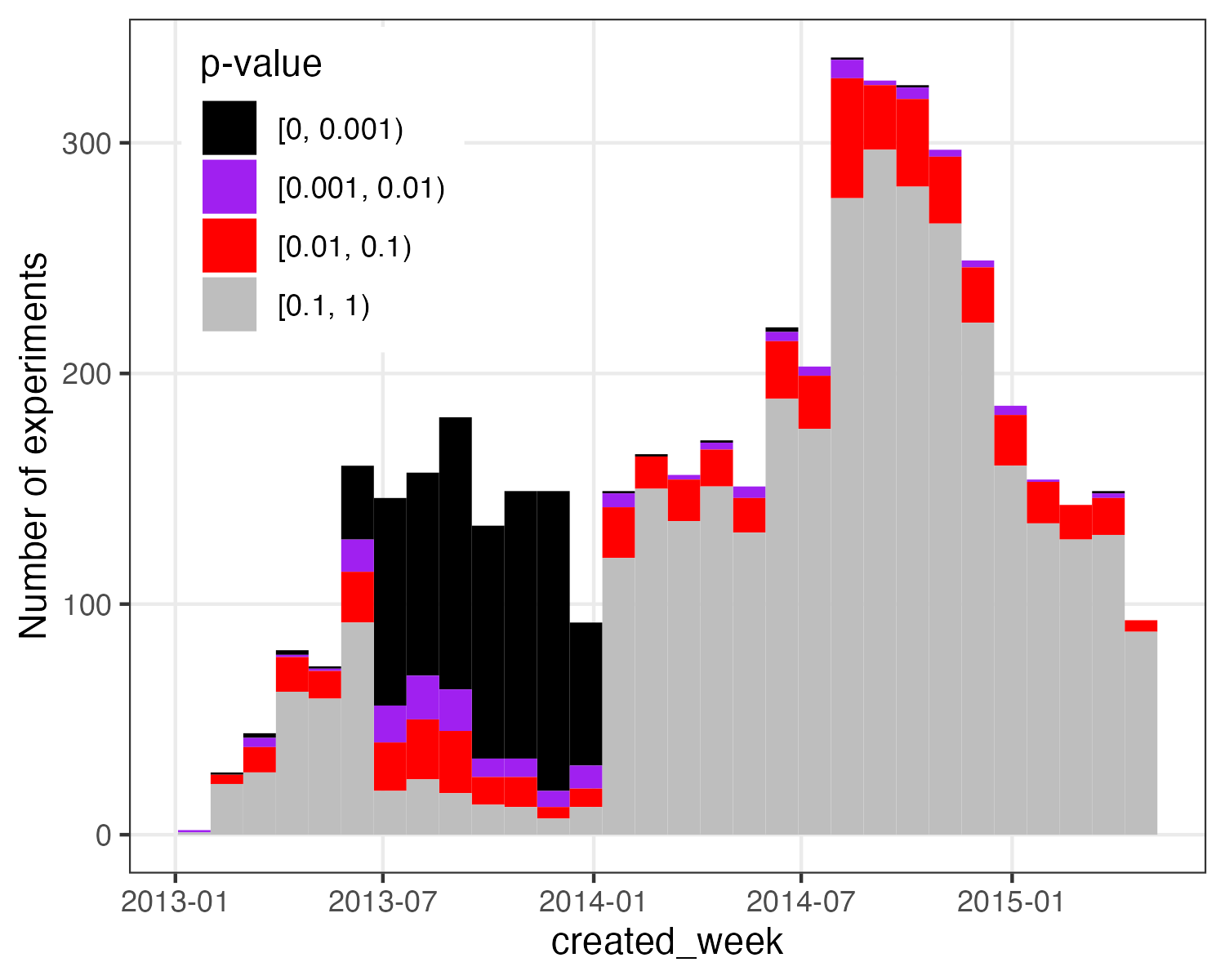
There were some problems with treatment randomization in the published data. In particular, Garrett Johnson pointed out to me that there were either too many or too few viewers assigned to one of the treatments (e.g. SRM). We followed up on this some more in 2021. (The analysis below is based on 4,869 experiments from an exploratory dataset with at least 1,000 observations.)

If we do a chi-square test on the proportions of each treatment, and zoom in on the interesting part, we get the following distribution of p-values:

That is, there are too many small p-values ​​compared to a uniform distribution. Or, more practically, there are many experiments that do not seem to have an appropriate number of observations in each condition. Some further analysis showed that these “bad” SRM experiments were particularly common among experiments made in certain time periods.

But it was difficult to say in detail why.

So in 2022, I reached out to Nathan Matias and Kevin Munger. They took this problem very seriously, but they also did not conduct these experiments or build the tools used to do them, making it difficult to investigate the problem.

Well, last week they Results were announced publicly their investigation. They hypothesize that this problem is caused by some caching, which may result in subsequent visitors to a particular core article page seeing the same treatment headlines for other articles. This creates a strange kind of autocorrelated randomization. Perhaps the point estimate may still be unbiased and consistent, but the inference assuming independent randomization may be wrong.

I’ve personally never encountered this kind of caching problem in the experiments I’ve investigated. This can cause other caching issues, such as new processing causing more cache misses, slowing things down enough that some logging doesn’t occur. So this is probably a useful addition to your menagerie of random demons. (Some of these issues are discussed below: this paper Others.)

They identify a specific period (June 25, 2013 to January 10, 2014) in which this issue was concentrated.

Prior to publication, Nathan and his colleagues contacted several teams that had published research using this remarkable collection of experiments. Excluding data from the period when SRM was particularly high (accounting for 22% of experiments), these teams generally didn’t see much change in their core results, which is good.

What are the remaining issues?

I took another look at the entire data set from the experiment. Outside of periods when the problem is concentrated, there are still too many SRMs. Of the experiments outside this period, 113 had SRM p-values ​​< 0.001. The 95% confidence interval is 0.45%. [0.37%, 0.54%], so this is clearly an excess for such an unbalanced experiment (compared to the 0.1% expected under the null). It is even less than the bad period (where this value is ~2/3). The problem is more severe before than after the acute phase. This makes sense if the team has addressed the root cause.

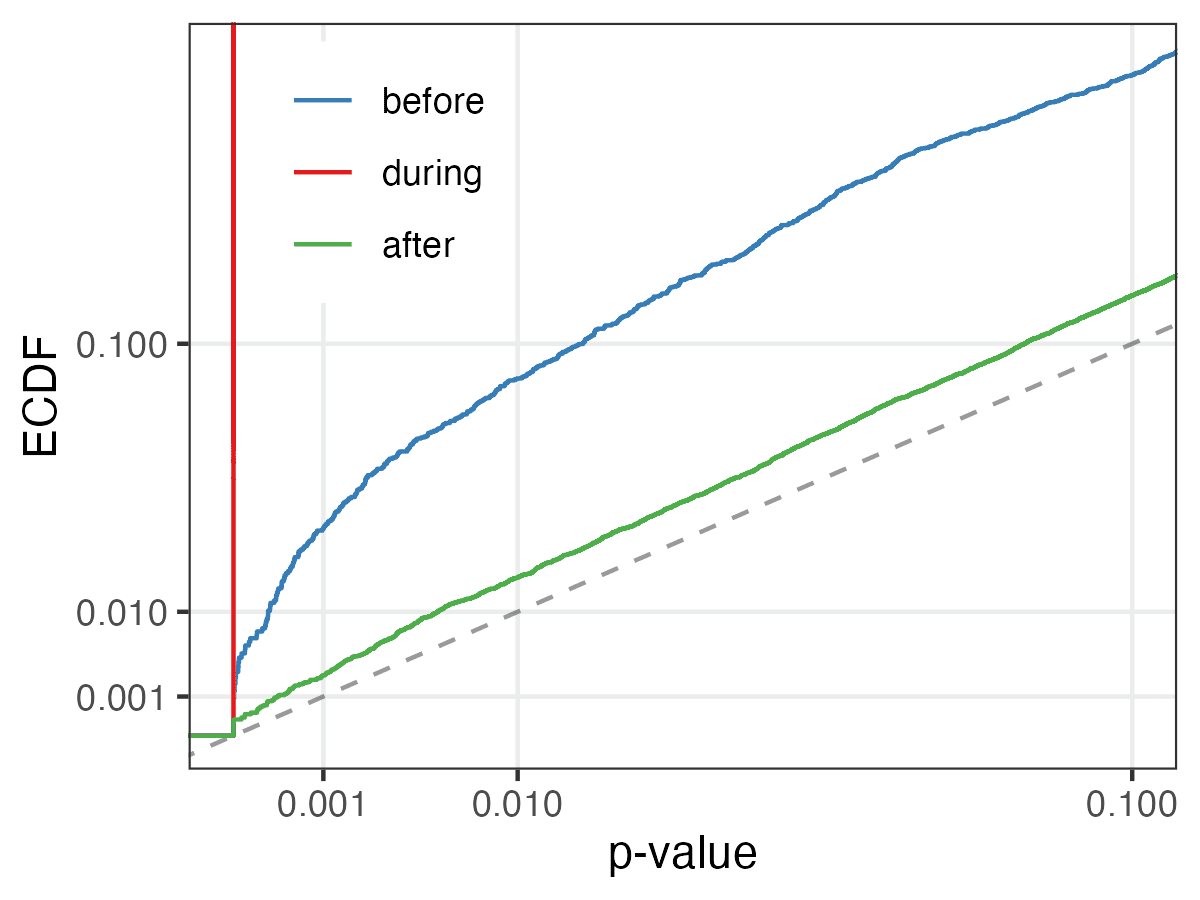
If there are only about 0.5% of the remaining experiments that are problematic, it is likely that many uses of this data will not be affected. In the end, removing 22% of the experiments did not significantly affect the conclusions of the other tasks. But of course, we cannot necessarily know that we have the power to detect all violations of the null hypothesis of successful randomization (including some that may invalidate the results of that experiment). But overall, compared to not doing these tests, we think we have more reason to be confident about the remaining trials, especially the post-acute trials.

I hope this will be an interesting case study that further demonstrates how widespread and troublesome the randomization problem is. And there may be another example coming soon.

[This post is by Dean Eckles. Because this post discusses practices in the Internet industry, I note that my disclosures include related financial interests and that I’ve been involved in designing and building some of those experimentation systems.]