It is common to correlate term spreads with future economic activity measured in one way or another. A recession in the US appears to be predictable based on term spreads. However, as defined by NBER, ECRI, and others, a recession is a binary variable. What about growth as a continuous variable, such as GDP growth or industrial production growth?
Chin and Cuco (2015) The predictive power of the 10-year-3-month spread for industrial production growth appears to have decreased over time, with the slope coefficient being statistically significant in 1970–97 but not in 1998–2009. What about the most recent data? The Bai-Perron sequential break test using quarterly data from 1967 to 2023Q3 (and thus a recession indicator through 2024Q3) indicates a break in 1984Q2. The slope coefficient is very important initially, but not later on.
What can we say about whether the slope coefficient has predictive power for some indicators and not for others? In general, the proxy for growth at a monthly frequency was industrial production. This is because industrial production was the only long-term indicator available. However, now that we have a variety of indicators, we can now evaluate the predictive power of spreads (and other financial indicators) on monthly data.
Here we compare monthly GDP from S&P Global (formerly IHS-Markit, Macroeconomic Advisers) with the Philadelphia Fed’s Industrial Production Coincident Index. The dependent variable is the year-over-year growth rate calculated using log differences.
Figure 1: Industrial production growth rate compared to the previous year (black), monthly GDP growth rate (light blue), and coincident index (yellow brown). NBER defines recession dates as gray, from peak to trough. Sources: Federal Reserve Bank and Philadelphia Fed via FRED, SPGMI (released November 1), NBER, and author’s calculations.
All three indicators are revised over time, but the monthly GDP and coincident index are revised substantially on a recurring basis (as are the official quarterly GDP series).
Therefore, the industrial production growth rate deviates significantly from the GDP growth rate compared to the previous year. This is even more true when looking at m/m, as seen in Figure 2 (we have reduced the extreme movements of IP to -6% m/m < growth < +6% m/m).

Figure 2: Scatter plot of m/m growth rate of monthly GDP versus monthly industrial production for the range -6% m/m < IP growth rate < +6% m/m (blue circles) and nearest neighbor fit (red line).
Table 1 presents the results of estimating the relationship for the typical 1992-2023M08 sample (so the last observation on the dependent variable is the y/y growth rate in 2024M08). 1992 is the starting point because monthly GDP is not available before then. The first three columns report simple bivariate regressions, and the next three columns expand the term spread using the Chicago Federal Reserve National Financial Conditions Index and debt service ratios (see: Chin and Ferrara (2024) For more information on the latter, see BIS).
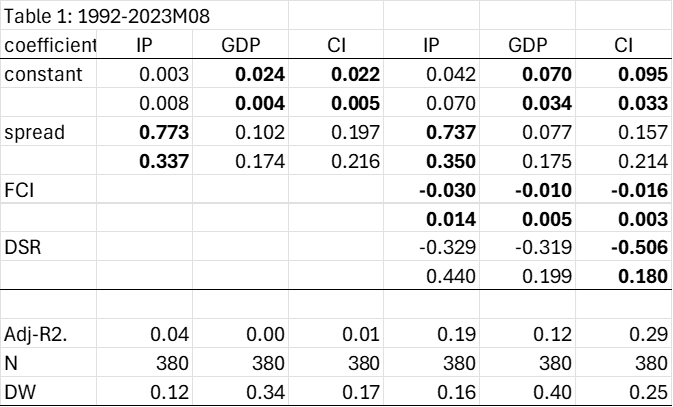
Note: The dependent variable is the 12-month log difference of industrial production (IP), monthly gross domestic product (GDP), or coincident index (CI). Spread is the 10-year to 3-month Treasury spread in bps, FCI is the Chicago Fed National Financial Conditions Index, and DSR is the private non-financial sector debt service ratio (in decimal format). Bold indicates statistical significance at 5% msl using Newey-West robust standard errors. Source: Author’s calculations.
Spreads are a statistically significant determinant of industrial production growth rates, but the proportion of variance explained is extremely low. Interestingly, this finding of significant coefficients does not apply to monthly GDP or coincident indices (factors primarily based on labor market indicators).
Enhancing specifications with FCI and DSR will significantly impact IP growth. FCI also significantly affects GDP growth and CI growth, the difference being that in both cases the spread is not statistically significant. DSR is only significant for the matching index.
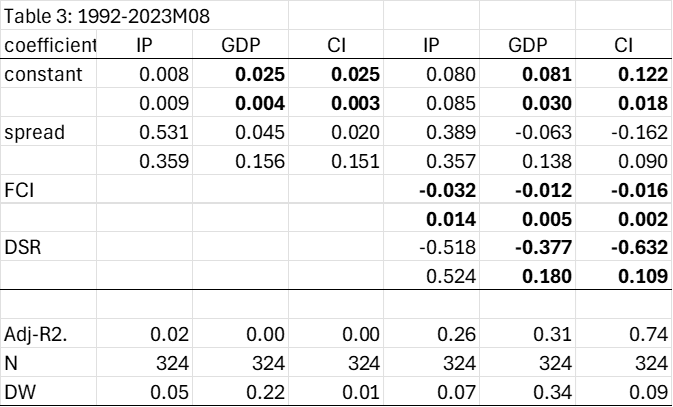
One may wonder whether including the pandemic period may distort the results. To check this, let’s delete the 2019M01~2020M12 interest rate data.

Note: The dependent variable is the 12-month log difference of industrial production (IP), monthly gross domestic product (GDP), or coincident index (CI). Spread is the 10Y-March Treasury spread in bps, FCI is the Chicago Fed National Financial Conditions Index, and DSR is the private non-financial sector debt service ratio (in decimal format). Bold indicates statistical significance at 5% msl using Newey-West robust standard errors. Source: Author’s calculations.
Now the spread does not enter significantly in any of the specifications (although it is significant at 10% msl for the bivariate IP spread regression). In fact, the significance of the spread seems to be a product of the pandemic period. For the pre-pandemic sample, we obtain the following estimates:
Note: The dependent variable is the 12-month log difference of industrial production (IP), monthly gross domestic product (GDP), or coincident index (CI). Spread is the 10Y-March Treasury spread in bps, FCI is the Chicago Fed National Financial Conditions Index, and DSR is the private non-financial sector debt service ratio (in decimal format). Bold indicates statistical significance at 5% msl using Newey-West robust standard errors. Source: Author’s calculations.
It has been standard practice to use industrial production as a proxy for the broader aggregate, but this is not economically motivated, it is almost a convenience. Industrial production (mining, utilities and manufacturing) was only 13% of GDP in 2023. Therefore, to examine the impact of financial indicators on aggregate economic activity, it makes more sense to focus on GDP.
The bottom line is that the term spread predicts IP growth but does not predict overall economic activity over the past 30 years. Interestingly, Ahmed and Chin (2024)Foreign term spreads predict GDP.






